ARAL基础数据类型说明

1. 数据类型

ARAL 定义了4个基础数据类型:

using Vector6d = std::array<double, 6>;
using VectorNd = std::array<double, ARAL_ROBOT_DOF>;    // ARAL_ROBOT_DOF 表示机械臂的自由度数

typedef Vector6d                            RLPose;         
typedef Vector6d                            RLTwist;        
typedef Vector6d                            RLWrench;       
typedef VectorNd                            RLJntArray;

i. RLPose

RLPose 描述笛卡尔空间的位姿, 前三个元素表示位置, 后三个元素表示姿态, 姿态采用RPY角来描述.

可以作定义 RLPose　T_b_a = [x, y, z, rx, ry, rz]　其中:

  • T_b_a : 为坐标系 a 在坐标系 b 的相对位姿描述

  • x, y, z: 为坐标系Ａ在坐标系b中的位置描述

  • rx, ry, rz: 为坐标系Ａ的在坐标系b中的姿态描述

RPY欧拉角可以描述为:

  • 转动坐标轴的顺序为：X->Y->Z, 以固定坐标系的姿态作为参考(固定模式)，即先绕固定坐标系X轴旋转$\gamma$，再绕固定坐标系Y轴旋转$\beta$，再绕固定坐标系Z轴旋转$\alpha$，如下图所示。（需要注意与浮动模式的区别）
  • 以右手法则为准，拇指指向为轴正方向，四指转向为角度正方向。

计算公式如下： R(RX,RY,RZ)=Rot(z,α)Rot(y,β)Rot(x,γ) R(R_X,R_Y,R_Z) = Rot(z,\alpha)Rot(y,\beta)Rot(x,\gamma) 固定模式在数学表达式上表现为旋转矩阵左乘，浮动模式在数学表达式上表现为旋转矩阵右乘。两者的主要区别如下图所示:

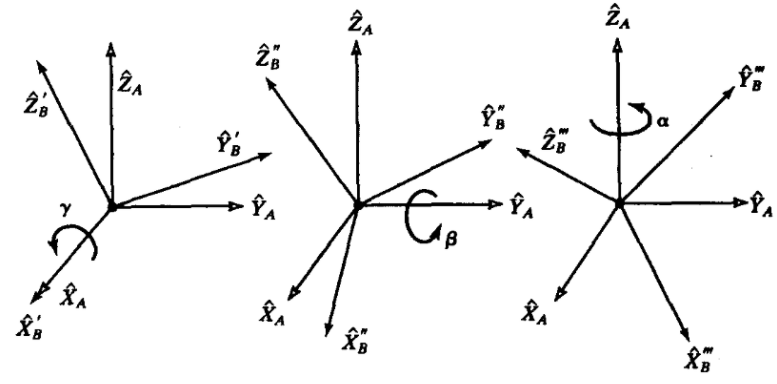
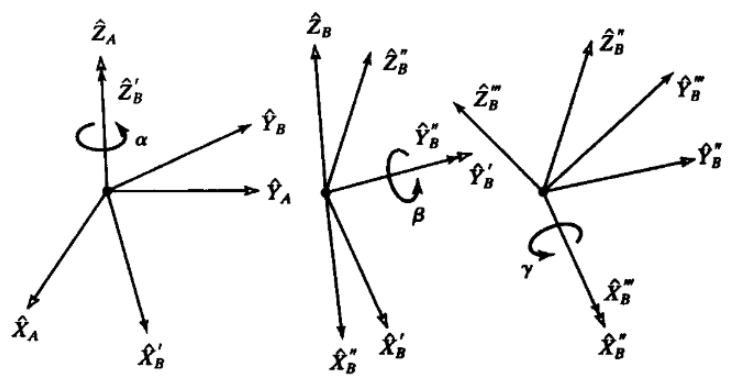
image-20210126163623147 image-20210126163520130

​ XYZ固定欧拉角（RPY） ZYX浮动欧拉角

要确定一个刚体在空间的位姿，须在物体上固连一个坐标系，然后描述该坐标系的原点位置和它三个轴的姿态，总共需要六个自由度或六条信息来完整地定义该物体的位姿。

理解欧拉角时，应该结合两个维度。1）旋转顺序（XYZ、ZYZ等); 2）参考坐标系（固定模式或者浮动模式）

ii. RLTwist

RLTwist 描述笛卡尔空间的广义速度, 前三个元素表示线速度, 后三个元素表示角速度。

可以作定义 RLTwist V_b_a = [vx, vy, vz, wx, wy, wz] , 其中：

  • V_b_a: 为坐标系 a 的广义速度在坐标系 b 的描述

  • vx, vy, vz: 为 坐标系 a 的 线速度

  • wx, wy, wz: 为坐标系 a 的 角速度

iii. RLWrench

RLWrench 描述笛卡尔空间的广义力, 前三个元素表示力, 后三个元素表示力矩。

可以作定义 RLWrench F_b_a = [fx, fy, fz, tx, ty, tz] , 其中：

  • F_b_a : 为作用在坐标系 a 的力和力矩在在坐标系 b 的描述

  • fx, fy, fz: 为 作用在坐标系 a 的力

  • tx, ty, tz : 为作用在坐标系 a 的矩

iv. RLJntArray

描述机械臂关节空间的量; 表示和机械臂关节角相关的量, 例如关节位置, 速度, 加速度, 关节力矩, 力矩常数等;

2. 参数单位

如没有特殊说明, 所有参数均采用标准单位

算法库中的标准单位有:

  • 时间: 秒(s)
  • 线位移(距离): 米(m)
  • 线速度: 米每秒(m/s)
  • 线加速度: 米每二次方秒(m/s^2)
  • 角位移(角度): 弧度(rad)
  • 角速度: 弧度每秒(rad/s)
  • 角加速度: 弧度每二次方秒(rad/s^2)
  • 力: 牛顿(N)
  • 力矩: 牛米(Nm)
  • 质量: 千克(kg)
  • 电流: 安培(A)
  • 力矩常数: Nm/A

results matching ""

    No results matching ""